本期题目：行测判断推理题目

题目一：数量规律

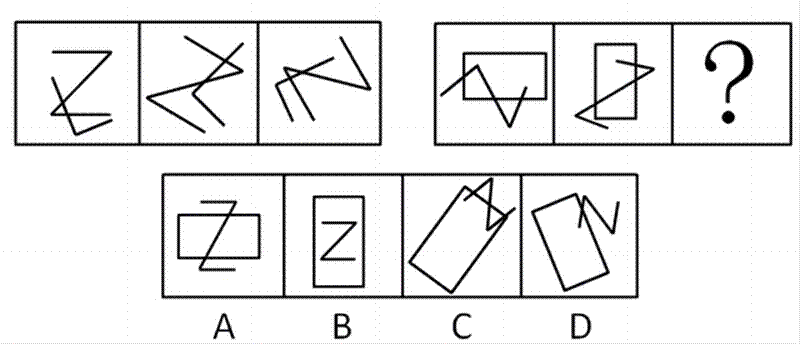
1. 从所给四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：

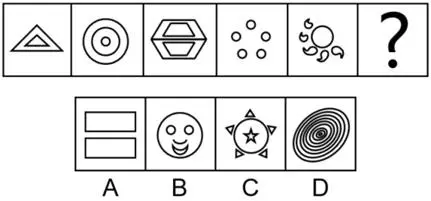
2. 请从所给的四个选项中，选择最合适的一项填在问号处，使之呈现一定的规律：

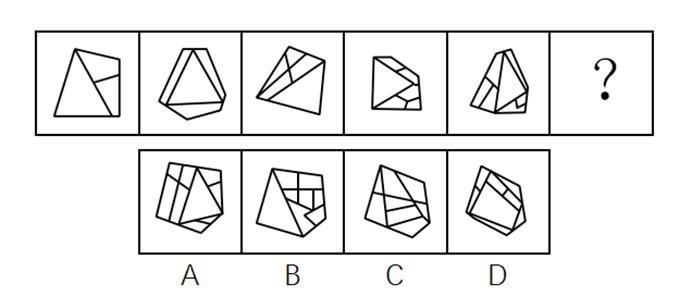
3. 从所给的四个选项中，选择最合适的一个填入问号处， 使之呈现一定的规律性：

4. 从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

本期答案及解析

1. C 观察图形交点明显，都是两个图形且相交的。第一组图形中，两图交点数量都为2；第二组图形，两图交点数量为3，那么第三个图形的交点数量也应为3，只有C符合。

2. B 组成元素不同，优先考虑数量类或属性类，线条的特征比较明显，考虑数线。九宫格，横向规律较为常见，优先考虑。第一行图形的线条数依次为1、2、3，呈等差规律，第二行图形的线条数依次为4、5、6，符合规律，第三行图形的线条数依次为7、8，问号处图形的线条数应为9，只有B项符合。

3. C 题干图形元素组成不同，且封闭面明显，“窟窿”较多，考虑数面。题干面数量依次为2、3、4、5、6、？，故“？”处应该选择面数量为7的图形，对应C项。

4. B 图形分割明显，可以考虑面数量规律。面数量分别为3、4、5、6、7、？，问号处需填8个面的图形，选项面数量分别为9、8、8、8，排除A项。考虑面考点细化发现，每个图形被分割最大面均为三角形，故答案为B。

本期涉及知识点

一、点数量

在图形推理中，只需考虑线条相交得到的点（即交点），不考虑端点，下面五幅图中标灰的点就是交点。

交点中有一类特殊的点——切点，即由相切关系得到的交点，如图5，共有3个交点，其中有2个点为切点。

当有以下特征图时，可能考察点的数量规律

1.线条交叉明显（比如米字形）

2.绕来绕去的一团线

3.切点（或顶点）较多

注意考察点的形式：比如曲直交点、曲曲交点、直直交点

数点情况：

1.整体数点：

但只看内部角数量无规律时，可以考虑数外部的角但此种考法较为特殊（绝大多数题目只考内角），不常见，一般不优先考虑。

角还可以细分为锐角、直角和钝角。

扇形、多边形故意留缺口也可以看作角、优先考虑数角。

图形中出现直角时（H、工、T字型的修正和相似图形，电话卡图形），可优先关注直角。

五、元素（部分）数量

元素，可细分为个数、种类数和部分数3种情况，需要注意：连在一起的算作一部分。

图1，元素的个数是5，元素种类数是3（正方形、五角星、圆），部分数是5；

图2，元素的个数是5，元素种类数是4（正方形、五角星、圆、桃心），部分数是5

图3，元素的个数是3，元素种类数是3（五角星、四角星、椭圆），因为这三种小元素都连在了一起，因此部分数是1

当图形由很多独立的小元素构成时，可优先考虑数素，可以数元素的个数、种类；出现黑色粗线条图形或者生活化图形（如品牌logo等），优先数部分数。

六、笔画

题型：大部分考一笔画图形或者笔画数量呈等差

笔画数的特征图：五角星、“日”字及其变形、“田”字及其变形、多圆相切、多圆相交以及出现大量端点时，优先考虑笔画数

如何判断图形最少可以通过几笔画出来？

对于简单图形，可通过画图的方式直接得出，而对于复杂图形，可通过下列公式进行计算：

连通图的笔画数=奇点数÷2。其中含0个奇点的连通图可一笔画完成。

连通图

如果图中任意两点都是连通的，那么该图被称作连通图。这一概念很专业，实际做题时，可大致理解为图形中的线条连在了一起。

奇点

若以一个点为起点，延伸出的线条数为奇数，则该点为奇点。

偶点：若以一个点为起点，延伸出的线条数为偶数，则该点为偶点。

注意：奇点包括端点！